【シリーズ第2回】動かして理解する！実践的セグメンテーション：PCAと因子分析の徹底比較と戦略的使い分け

AI・機械学習

1. はじめに：分析アプローチの選択がビジネスの成果を左右する

顧客セグメンテーションを実行する際、多次元データからの特徴抽出は不可欠なプロセスである。その代表的なアプローチとして主成分分析（PCA）と因子分析が挙げられるが、両者は似て非なるものである。

PCAはデータの分散を最大化する「客観的な要約」を目指す一方、因子分析は変数間の共分散構造から「解釈可能な潜在因子」を見出すことを目的とする。この選択は、後続のクラスタリングや、最終的に得られるビジネスインサイトの質に直結する。

本稿では、同一のサンプルデータを用いて両アプローチを並行して実行。それぞれの特性とアウトプットの違いを明確にし、データサイエンティストが「ビジネス課題に応じて最適な手法を選択する」ための実践的な指針を提示する。

2. 分析対象データセット

本稿では、架空のECサイト「TokioMart」の顧客データを分析対象とする。データには、顧客の「行動変数」と「意識変数（アンケート結果）」が含まれており、実務においても頻繁に見られる構成としている。

tokiomart_customersサンプルデータダウンロード

▼分析データ概要

変数区分変数名データ型説明
行動変数月間平均利用額数値一人あたりの月間平均購入金額
行動変数月間平均訪問回数数値一人あたりの月間平均サイト訪問回数
意識変数価格重視度7段階評価「価格を非常に重視する」=7
意識変数品質重視度7段階評価「品質を非常に重視する」=7
意識変数トレンド重視度7段階評価「トレンドを非常に重視する」=7

3. アプローチ1：主成分分析（PCA）による客観的セグメンテーション

まず、データの構造を客観的に要約するPCAからアプローチする。PCAは、変数間の相関を考慮しながら、データ全体のばらつき（分散）を最もよく表現する新しい合成変数（主成分）を作り出す手法である。

▼Pythonによる実装

Python

Python
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
import seaborn as sns

!pip install japanize_matplotlib #初回のみインストール
import japanize_matplotlib # 日本語化ライブラリのインポート

# 事前に生成したサンプルCSVを読み込む
customer_data = pd.read_csv('tokiomart_customers.csv')

# 分析に使用する変数を選択
features = ['月間平均利用額', '月間平均訪問回数', '意識_価格重視度', '意識_品質重視度', '意識_トレンド重視度']
X = customer_data[features]

# データを標準化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# PCAの実行（2つの主成分を抽出）
pca = PCA(n_components=2, random_state=42)
X_pca = pca.fit_transform(X_scaled)

# 主成分スコアでk-meansクラスタリング（3つのクラスターに分類）
kmeans_pca = KMeans(n_clusters=3, random_state=42, n_init=10)
customer_data['cluster_pca'] = kmeans_pca.fit_predict(X_pca)

# 主成分のローディング（各主成分と元の変数の関係）を確認
loadings_pca = pd.DataFrame(pca.components_.T, columns=['PC1', 'PC2'], index=features)
print("--- PCA Loadings ---")
print(loadings_pca)

# グラフ描画の準備
plt.figure(figsize=(15, 6)) # 図全体のサイズ設定

# ---------------------------------------------------------
# 1. 主成分ローディングプロット（変数と主成分の関係）
# ---------------------------------------------------------
plt.subplot(1, 2, 1) # 1行2列の左側に描画

# 係数（ローディング）の矢印とテキストを描画
for i, feature in enumerate(features):
    # 矢印を描画 (原点0,0から開始)
    plt.arrow(0, 0, pca.components_[0, i], pca.components_[1, i], 
              color='red', alpha=0.5, head_width=0.05)
    # 変数名テキストを描画 (矢印の少し先に配置)
    plt.text(pca.components_[0, i]*1.2, pca.components_[1, i]*1.2, 
             feature, color='darkblue', ha='center', va='center', fontsize=10)

# グラフの体裁を整える
plt.xlim(-1, 1)
plt.ylim(-1, 1)
plt.xlabel('PC1 (第1主成分)')
plt.ylabel('PC2 (第2主成分)')
plt.title('主成分ローディングプロット')
plt.grid(True)
plt.axhline(0, color='black', linewidth=0.5) # X軸線
plt.axvline(0, color='black', linewidth=0.5) # Y軸線

# ---------------------------------------------------------
# 2. PCAによるクラスタリング結果の散布図
# ---------------------------------------------------------
plt.subplot(1, 2, 2) # 1行2列の右側に描画

# 散布図の描画
# x軸: PCA第1成分, y軸: PCA第2成分, 色分け: クラスター
sns.scatterplot(x=X_pca[:, 0], y=X_pca[:, 1], 
                hue=customer_data['cluster_pca'], 
                palette='viridis', s=100, alpha=0.8)

# グラフの体裁を整える
plt.xlabel('PC1 (総合エンゲージメントレベル)') #自身で解釈が必要
plt.ylabel('PC2（コスパ重要指数）') #自身で解釈が必要
plt.title('PCA空間上のクラスタリング結果')
plt.grid(True)
plt.legend(title='Cluster', loc='upper right')

# グラフを表示
plt.tight_layout()
plt.show()

▼結果と解釈

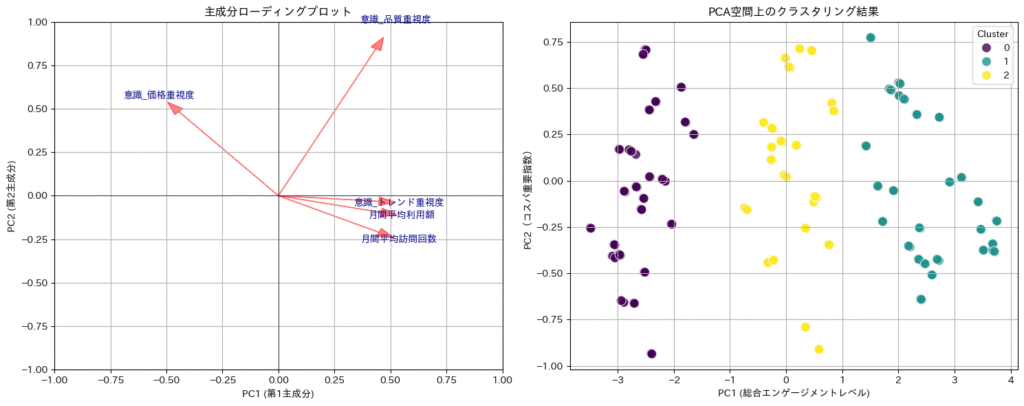
PCAの結果、第1主成分（PC1）は「利用額」「訪問回数」「品質重視度」「トレンド重視度」と強い正の相関を持ち、「価格重視度」とは負の相関を持つことがわかる。これは顧客の「総合的なエンゲージメントレベル」を示す量的指標と解釈できる。

この主成分スコアに基づきk-meansクラスタリングを実行した結果、以下の3つのセグメントが形成された。

クラスター (PCA)特徴命名
0PC1スコアが突出して高い。全ての行動・意識変数が高水準。コア顧客層
1PC1スコアが平均的。PC2スコアはやや低め。ミドル顧客層
2PC1スコアが低い。エンゲージメントが低い傾向。ライト顧客層

PCAは、観測変数から客観的な基準で顧客を序列化し、量的・構造的なグルーピングを行う上で非常に有効なアプローチである。

4. アプローチ2：因子分析による解釈的セグメンテーション

次に、変数間の共分散構造の背後にある潜在的な構造を探る因子分析でアプローチする。この手法は、観測された行動や意識が、直接は見えないいくつかの共通因子によって引き起こされている、というモデルを仮定する。

▼Pythonによる実装

※因子分析にはfactor_analyzerライブラリの利用を想定

Python

Python
!pip install factor_analyzer #初回のみインストール
from factor_analyzer import FactorAnalyzer

# 因子分析の実行（2つの因子を抽出、バリマックス回転）
# 因子数は事前にカイザー基準やスクリープロットで検討することが望ましい
fa = FactorAnalyzer(n_factors=2, rotation="varimax", method='principal')
X_fa = fa.fit_transform(X_scaled)

# 因子得点でk-meansクラスタリング
kmeans_fa = KMeans(n_clusters=3, random_state=42, n_init=10)
customer_data['cluster_fa'] = kmeans_fa.fit_predict(X_fa)

# 因子負荷量（各因子と元の変数の関係）を確認
loadings_fa = pd.DataFrame(fa.loadings_, columns=['Factor1', 'Factor2'], index=features)
print("\\n--- Factor Analysis Loadings ---")
print(loadings_fa)

# --- 因子分析の結果と解釈のためのグラフ描画  ---

# グラフ描画の準備
plt.figure(figsize=(15, 6)) # 図全体のサイズ設定

# ---------------------------------------------------------
# 1. 因子負荷量のヒートマップ
# ---------------------------------------------------------
plt.subplot(1, 2, 1) # 1行2列の左側に描画

sns.heatmap(loadings_fa, annot=True, cmap='viridis', fmt=".2f", linewidths=.5, cbar=True)
plt.title('因子負荷量のヒートマップ')
plt.xlabel('因子')
plt.ylabel('変数')
plt.tight_layout()

# ---------------------------------------------------------
# 2. 因子分析によるクラスタリング結果の散布図
# ---------------------------------------------------------
plt.subplot(1, 2, 2) # 1行2列の右側に描画

# 散布図の描画
# x軸: 第1因子, y軸: 第2因子, 色分け: クラスター
sns.scatterplot(x=X_fa[:, 0], y=X_fa[:, 1], 
                hue=customer_data['cluster_fa'], 
                palette='viridis', s=100, alpha=0.8)

# グラフの体裁を整える
plt.xlabel('Factor1 (非価格重視因子)')
plt.ylabel('Factor2 (付加価値追求因子)')
plt.title('因子空間上のクラスタリング結果')
plt.grid(True)
plt.legend(title='クラスター', loc='upper right')

# グラフを表示
plt.tight_layout()
plt.show()

▼結果と解釈

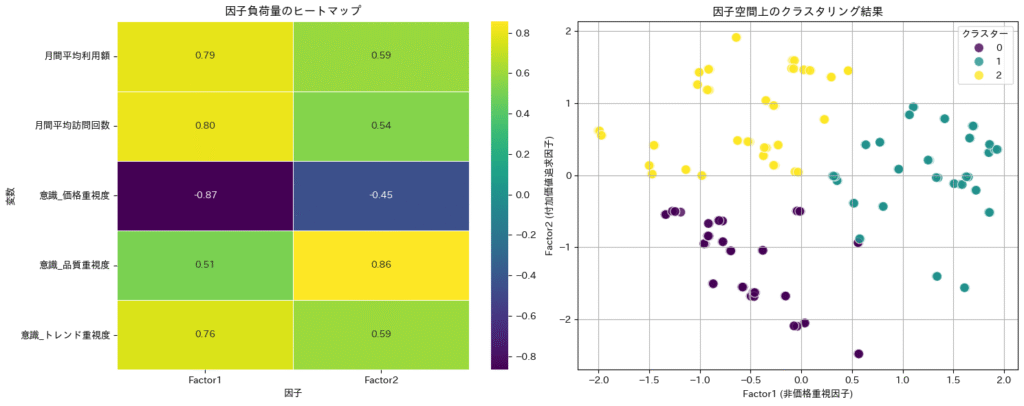
因子分析の結果、2つの潜在因子が抽出された。第1因子は「価格重視度」と強い負の相関、「利用額」「訪問回数」と強い正の相関があることから「非価格重視」因子と命名する。第2因子は「品質重視度」と関連が深いことから「付加価値追求」因子と命名する。

これらの因子得点に基づきクラスタリングした結果、全く異なる切り口の3セグメントが形成された。

クラスターFactor1 (X軸: 非価格重視)Factor2 (Y軸: 付加価値追求)特徴命名案
0 (紫色)低い低い節約・価格重視顧客
(価格重視, 低利用)(低品質・トレンド志向)価格を重視し、利用頻度や付加価値への関心も低い、最もエンゲージメントの低い層。
1 (緑色)高い高いロイヤル顧客
(価格非重視, 高利用)(高品質・トレンド志向)価格に左右されず、品質と利用頻度も高い優良顧客層。
2(黄色)低い高いコスパ顧客
(価格重視, 低利用)(高品質・トレンド志向)価格と品質の両立を求める堅実な顧客層。

因子分析は、顧客行動の背景にある動機や価値観といった質的なインサイトを抽出し、マーケティングペルソナに近いセグメントを構築する上で強力な手法である。

5. 総括と戦略的使い分けの指針

同一データから、全く異なる二つのセグメンテーションが生まれた。PCAは顧客をエンゲージメントの「量」で分け、因子分析は「価値観」で分けた。どちらが正しいという訳ではなく、ビジネス目的によってその有効性が決まる。

以下に、両アプローチの戦略的な使い分けの指針を示す。

結論として、予測や客観的な分類が主目的であればPCAを、顧客理解やマーケティング戦略立案が目的であれば因子分析を選択することが、より意図に沿った分析ができる。

6. 次回予告

手法の選択は、ビジネス課題によって決まる。今回はその重要な一例を示した。しかし、現実のデータは、必ずしもこのような線形的な手法で綺麗に分離できるとは限らない。

次回は、より複雑でカオスなデータの中から、意味ある顧客群を発掘する。非線形次元削減の主要手法であるUMAPと、密度ベースクラスタリングの進化形HDBSCANを組み合わせた、現代的な探索的データ分析の世界を解説する。

この記事が役に立ったと感じたら、ぜひSNSでシェアをお願いします！

Hiro｜データサイエンティスト

ベンダーと金融現場の“両サイド視点”でデータ活用を支援中。

X（旧Twitter）とLinkedInでも最新ネタを発信しています → @Hiro_data_fin

コメント

タイトルとURLをコピーしました